EP-MK1 Documentation

Created in November 12, 2019

2019   ·   plugins   documentation   synthesis   physical modelling

EP-MK1 is a synthesized electric piano made with Pure Data and Camomile.

The resulting sound is a combination of four layers:

  • Hammer Layer: the excitation source for the tone bar and tine layer.
  • Tone Bar Layer: the main component, a resonator filter oscillating at the fundamental frequency.
  • Tine Layer: two resonators with user-defined frequency ratios for each filter.
  • Pickup Layer: A sum of the three previous layers through a filtered nonlinear distortion.

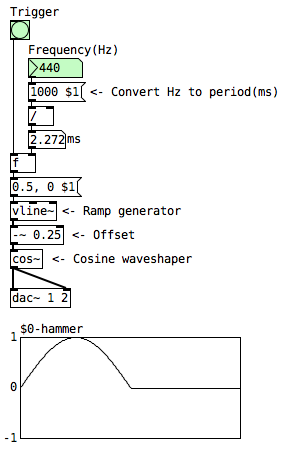
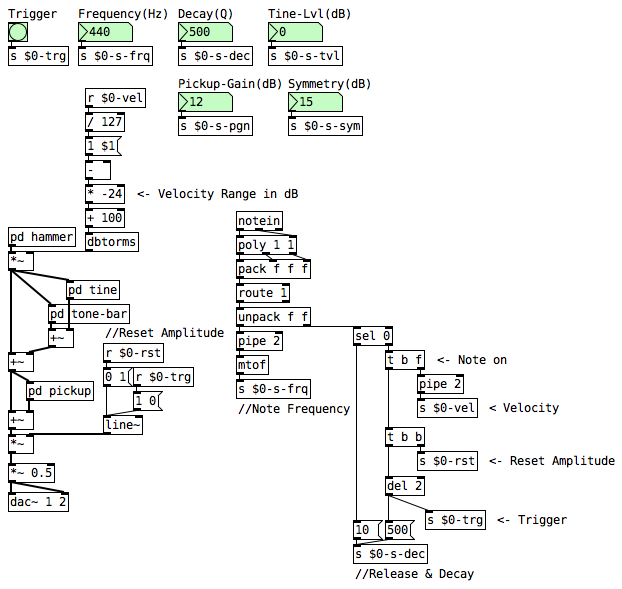
Hammer Layer

The hammer layer was synthesized using a high-precision audio ramp generator object vline~ going through a cosine waveshaper cos~. The result is a pulse with a length in milliseconds equal to one period of our fundamental frequency.

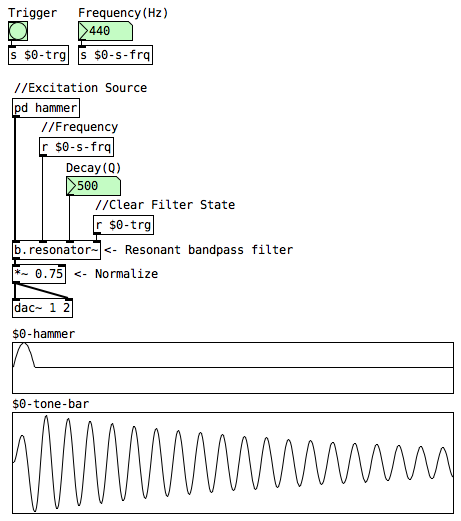
Tone Bar Layer

The tone bar’s only component is a resonant band-pass filter with constant skirt, better known as a resonator in modal synthesis. Sending a source of excitation to the resonator will output a decaying sine wave oscillating at the filter’s frequency. The sine wave’s decay time is determined by the filter’s resonance (Q).

In this instrument the abstraction b.resonator~ from the mkmr library is being used, but there are plenty of resonators to choose from for Pure Data:

The inlets parameters for b.resonator~ are the following:

  1. signal - signal to be filtered or excite the resonator.
  2. float - sets the central cutoff frequency in hertz.
  3. float - sets the filter’s resonance (Q).
  4. bang - reinitialize the filter’s internal state.

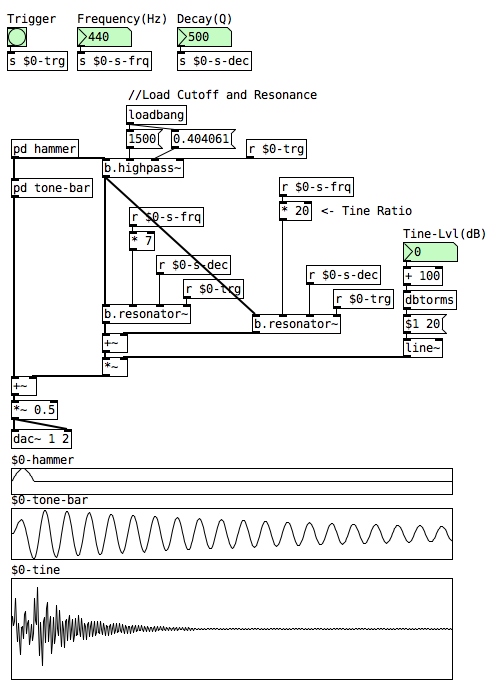
Tine Layer

The bell-like sound in an Electric Piano comes from the tine layer which is composed of two resonators being excited by a filtered hammer. First, the hammer goes through a 2-pole high-pass filter to remove any unwanted low frequency content like thumps or clicks. Then, the resonator’s frequency ratios are set to 7 and 20 to generate those harmonics respectively. Finally, a volume parameter is recommended to control the level of “brightness”.

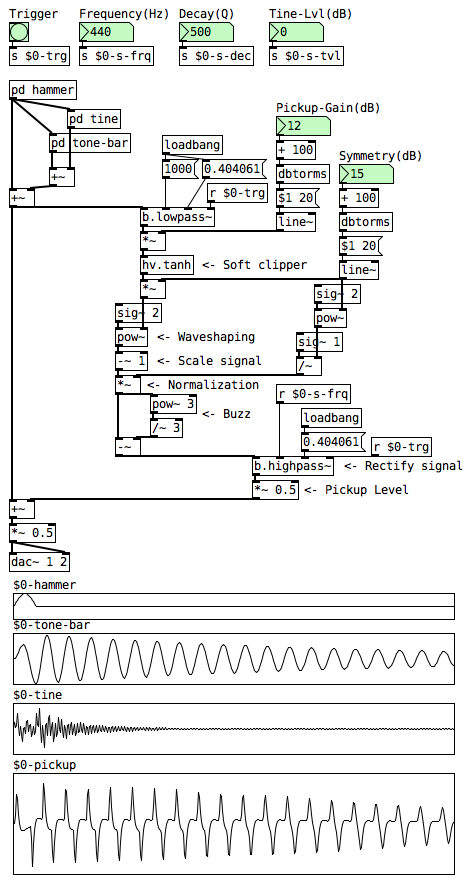
Pickup Layer

The pickup model is a parallel layer with nonlinear distortion. First, the sum of the three layers are sent to a 2-pole low-pass filter to get a cleaner tone on the higher notes. Then, the signal goes through a soft clipper which then goes a waveshaping process to enhance the even harmonics with the symmetry parameter. Finally, it gets normalized and rectified using a high-pass filter fundamental frequency.

MIDI Implementation

Lastly, MIDI is implemented to control the fundamental frequency, the hammer’s amplitude and the resonator’s decay and release time. It is important to reset the amplitude by setting it to zero on the first millisecond and then back to one on the second while simultaneously triggering the hammer and resetting the filters. This will avoid unwanted clicks and keep consistency at each trigger. Adding velocity control to the hammer’s amplitude will provide varied dynamics that affect the amount of harmonics produced by the pickup layer.

References